插入排序简介
插入排序的基本思想是,把 n 个待排序的元素看成一个有序表和一个无序表。
开始时,有序表中只包含一个元素,无序表中则包含 n-1 个元素。
排序过程中每次从无序表中取出第一个元素,将它插入到有序表中适当的位置,使之成为新的有序表。
只要重复 n-1 次,即可完成排序过程。
插入排序实现
下面选取插入排序的一个中间过程对其进行说明。
假设 {20,30,40,10,60,50} 中的前 3 个数已经排列过,是有序的了。接下来对 10 进行排列。
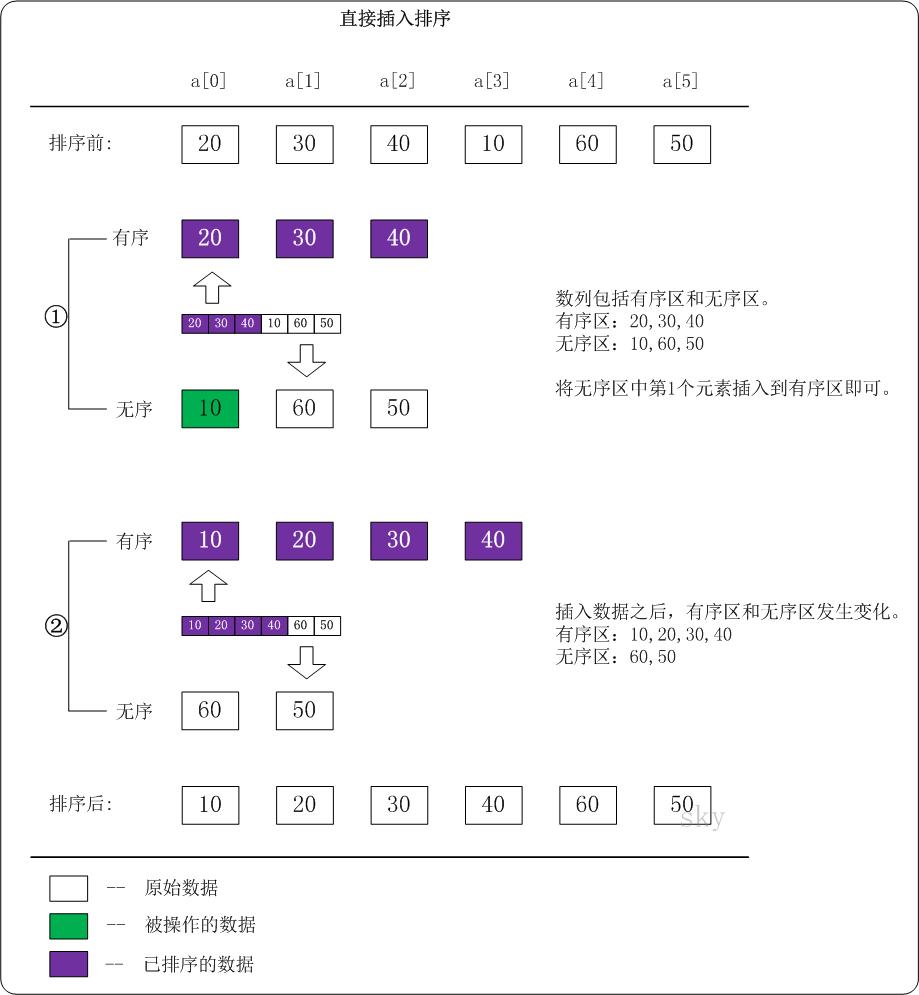
图中将数列分为有序区以及无序区。这里需要做的只是取出无序区中的第一个数,并找到它在有序区所对应的位置。若有必要的话,则对有序区中的相关数据进行移位。
复杂度与稳定性
插入排序时间复杂度
插入排序的时间复杂度是 。
假设要被排序的数列中有 N 个数,遍历一趟的时间复杂度为 。
由于算法需要遍历 N-1 次,因此插入排序的时间复杂度为 。
插入排序稳定性
插入排序是稳定的算法,其满足稳定算法的定义,即假设在数列中存在 a[i] = a[j],若 a[i] 在排序之前处在 a[j] 前面,并在排序之后仍处在 a[j] 前面,则该排序算法是稳定的。
代码实现
输入:arr 为要排序数列,n 为数列的元素个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void insertionSort(int* arr, int n) {
int i, j, k;
for (i = 1; i < n; i++) {
// 为 a[i] 在 a[0...i-1] 的有序区中找一个合适的位置
for (j = i - 1; j >= 0; j--) {
if (arr[j] < arr[i]) {
break;
}
}
// 若找到一个合适的位置
if (j != i - 1) {
// 将比 a[i] 大的数据往后移
int temp = arr[i];
for (k = i - 1; k > j; k--) {
arr[k+1] = arr[k];
}
// 最后将 a[i] 放在该位置上
arr[k+1] = temp;
}
}
}