快速排序简介
快速排序的基本思想是,选择一个基准数,通过一趟排序将要排序的数据分割成独立的两部分。
其中一部分的所有数据都比另外一部分的所有数据都要小。随后,再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序数列。
快速排序实现
首先,从数列中挑一个基准值,并将所有比基准值小的摆放在基准前面,所有比基准值大的都摆在基准后面。在这个分区退出后,该基准就处于数列的中间位置。之后,再递归地把基准值前面的子数列和基准后面的子数列进行排序即可。
下面以数列 a = {30, 40, 60, 10, 20, 50} 为例,演示快速排序的过程。
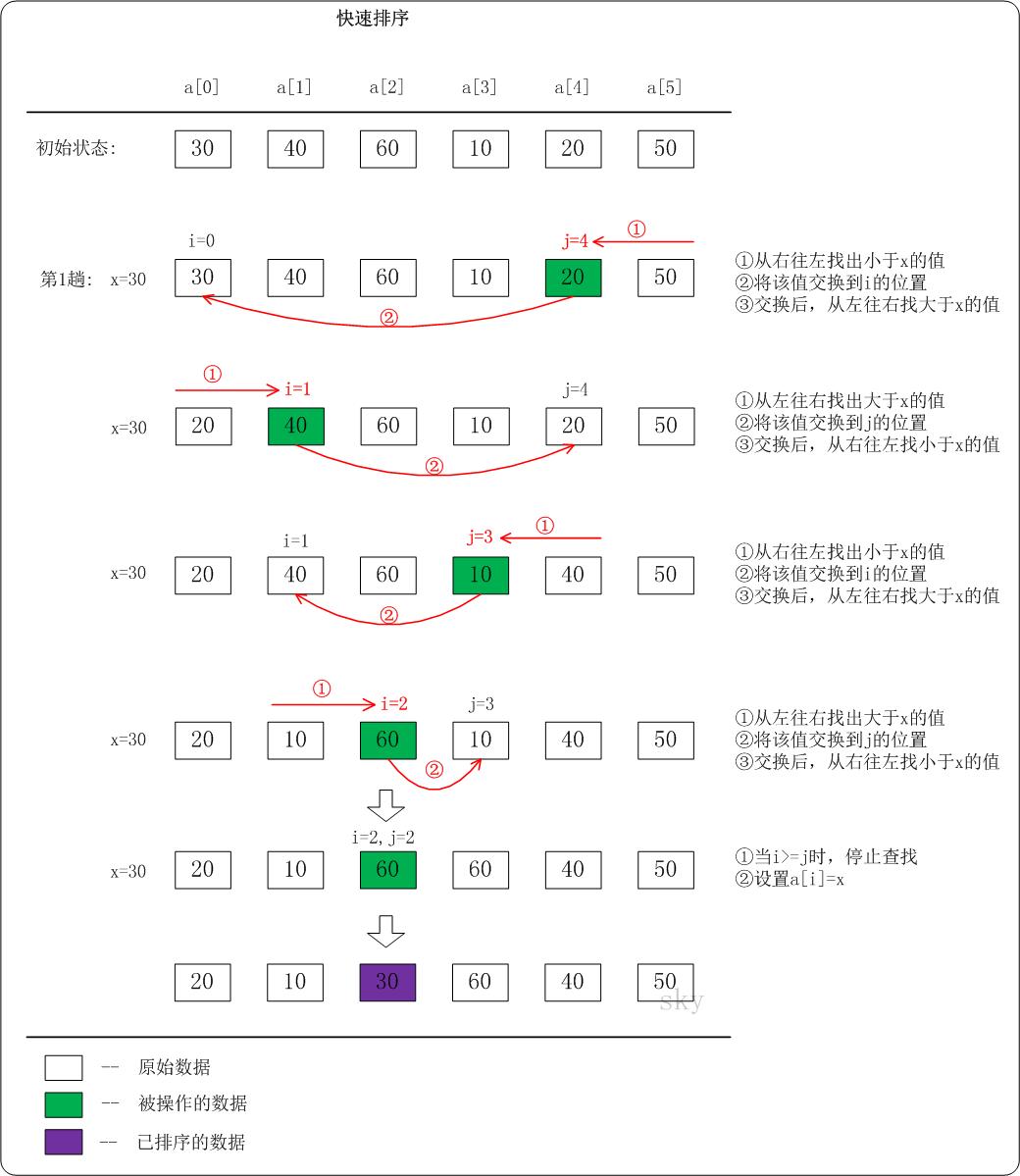
第一趟中,i = 0,j = 5,基准值 x 设为 a[i],即 x = 30。
首先由右向左查找小于 x 的数,找到满足条件的数 a[j] = 20。此时 i = 0,j = 4,将 a[j] 赋值给 a[i]。
接着由左向右查找大于 x 的数,找到满足条件的数 a[i] = 40。此时 i = 1,j = 4,将 a[i] 赋值给 a[j]。
接着由右向左查找小于 x 的数,找到满足条件的数 a[j] = 10。此时 i = 1,j = 3,将 a[j] 赋值给 a[i]。
接着由左向右查找大于 x 的数,找到满足条件的数 a[i] = 60。此时 i = 2,j = 3,将 a[i] 赋值给 a[j]。
接着由右向左查找小于 x 的数,没有找到满足条件的数。此时 i >= j,停止查找,并将 x 赋值给 a[i]。
按照同样的方法,对子数列进行递归遍历。最后就可以得到有序数列了。
复杂度与稳定性
快速排序时间复杂度
假设被排序的数列中有 N 个数,遍历一趟的时间复杂度为 。
快速排序采用分治法进行遍历,因此可以将它视为一棵二叉树,即所需要遍历的次数为二叉树的深度。
- 二叉树的深度至少是 ,因此快速排序的遍历次数最少是 次。
- 二叉树的深度最大是 ,因此快速排序的遍历次数最多是 次。
快速排序的时间复杂度在最坏情况下是 ,平均的时间复杂度是 。
快速排序稳定性
快速排序是不稳定的算法,其不满足稳定算法的定义,即假设在数列中存在 a[i] = a[j],若 a[i] 在排序之前处在 a[j] 前面,并在排序之后仍处在 a[j] 前面,则该排序算法是稳定的。
代码实现
输入:arr 为要排序数列,left 为要排序数列的开头下标,right 为要排序数列的末尾下标
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void quickSort(int* arr, int left, int right) {
if (left < right) {
int i, j, pivot;
i = left;
j = right;
pivot = arr[i];
while (i < j) {
while (i < j && arr[j] > pivot) {
j--;
}
if (i < j) {
arr[i++] = arr[j];
}
while (i < j && arr[i] < pivot) {
i++;
}
if (i < j) {
arr[j--] = arr[i];
}
}
arr[i] = pivot;
quickSort(arr, left, i-1);
quickSort(arr, i+1, right);
}
}