归并排序简介
根据具体的实现,归并排序包括由上往下和由下往上的两种方式。
由下往上的归并排序
将要排序的数列分成若干个长度为 1 的子数列,再将这些数列两两合并。
得到若干个长度为 2 的有序数列后,再将这些数列两两合并,得到若干个长度为 4 的有序数列。
重复以上操作直到合并成一个数列,就可以得到有序数列了。
由上往下的归并排序
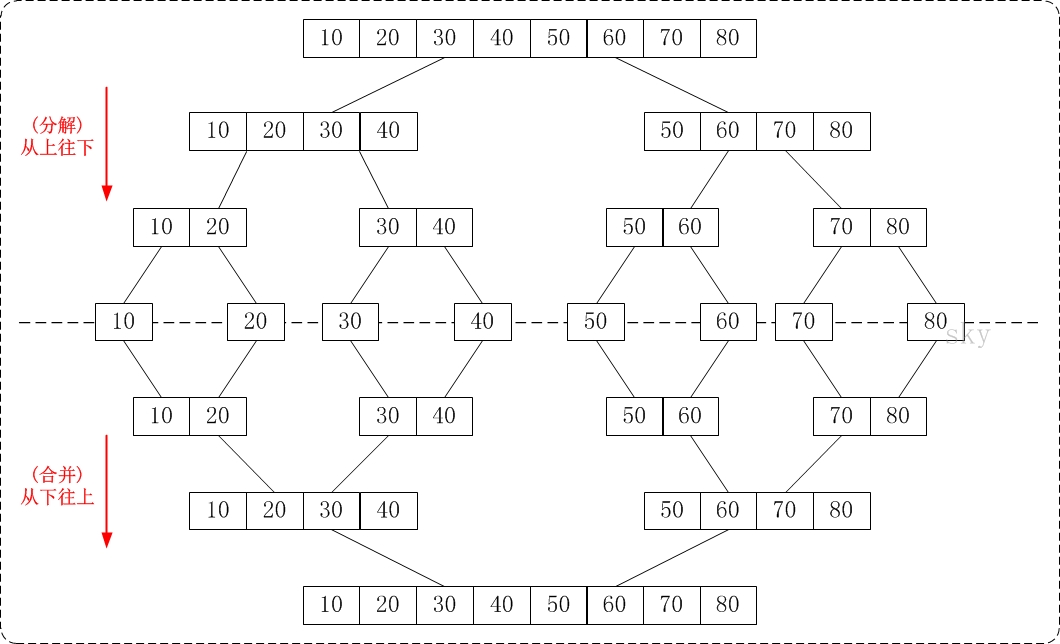
由上往下与由下往上在排序上是反方向的。它基本包括 3 个步骤:
分解 — 将当前区间一分为二,即求分裂点 mid = (low + high) / 2。
求解 — 递归地对两个子区间 a[low…mid] 和 a[mid+1…high] 进行归并排序,递归的终结条件是子区间的长度为 1。
合并 — 将已排序的两个子区间 a[low…mid] 和 a[mid+1…high] 归并为一个有序的区间 a[low…high]。
归并排序实现
由上往下的归并排序
由上往下的归并排序采用递归的方式实现。其原理如下图:
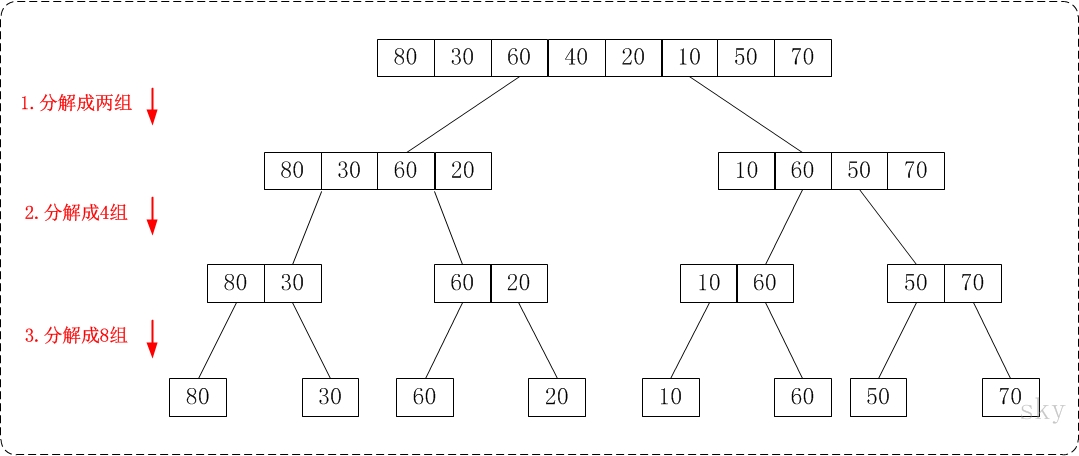
通过由上往下的归并排序来对数列 {80,30,60,40,20,10,50,70} 进行排序:
- 将数列 {80,30,60,40,20,10,50,70} 看作由两个有序的子数列 {80,30,60,40} 和 {20,10,50,70} 组成,对两个有序子数列进行排序即可。
- 将子数列 {80,30,60,40} 看作由两个有序的子数列 {80,30} 和 {60,40} 组成。
- 将子数列 {20,10,50,70} 看作由两个有序的子数列 {20,10}和{50,70} 组成。
- 将子数列 {80,30} 看作由两个有序的子数列 {80} 和 {30} 组成。
- 将子数列 {60,40} 看作由两个有序的子数列 {60} 和 {40} 组成。
- 将子数列 {20,10} 看作由两个有序的子数列 {20} 和 {10} 组成。
- 将子数列 {50,70} 看作由两个有序的子数列 {50} 和 {70} 组成。
由下往上的归并排序
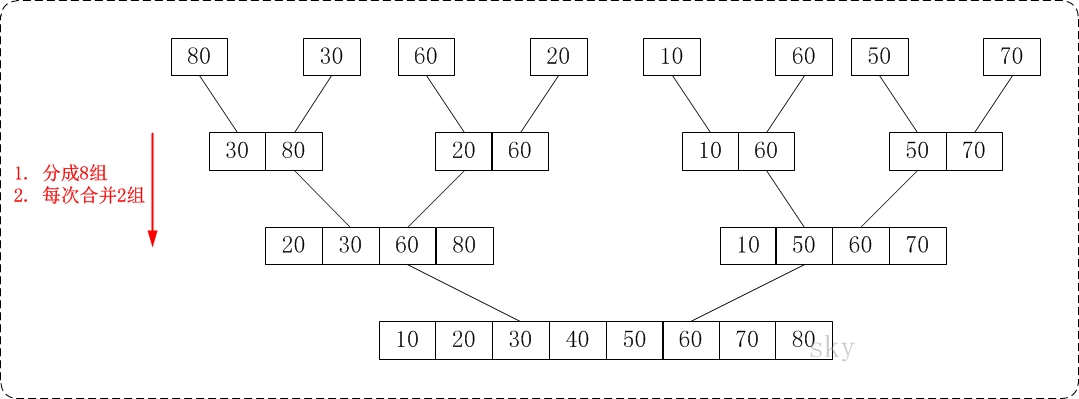
通过由下往上的归并排序来对数列 {80,30,60,40,20,10,50,70} 进行排序:
- 将数列 {80,30,60,40,20,10,50,70} 看作由 8 个有序的子数列 {80}, {30}, {60}, {40}, {20}, {10}, {50} 和 {70} 组成。
- 将这 8 个有序的子数列两两合并,得到 4 个有序的子数列 {30,80}, {40,60}, {10,20} 和 {50,70}。
- 将这 4 个有序的子数列两两合并,得到 2 个有序的子数列 {30,40,60,80} 和 {10,20,50,70}。
- 将这 2 个有序的子数列两两合并,得到 1 个有序的子数列 {10,20,30,40,50,60,70,80}。
复杂度与稳定性
归并排序时间复杂度
假设要排序的数列中有 N 个数,遍历一趟的时间复杂度为 。
由于归并排序的形式就像一颗二叉树,需要遍历的次数就是二叉树的深度。
根据完全二叉树,可以得出归并排序的时间复杂度为 。
归并排序稳定性
归并排序是稳定的算法,其满足稳定算法的定义,即假设在数列中存在 a[i] = a[j],若 a[i] 在排序之前处在 a[j] 前面,并在排序之后仍处在 a[j] 前面,则该排序算法是稳定的。
代码实现
由上往下的归并排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
void merge(int* arr, int left, int mid, int right) {
int* temp = (int*)malloc((right-left + 1) * sizeof(int));
int i = left;
int j = mid + 1;
int count = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[count++] = arr[i++];
} else {
temp[count++] = arr[j++];
}
}
while (i <= mid) {
temp[count++] = arr[i++];
}
while (j <= right) {
temp[count++] = arr[j++];
}
for (i = 0; i < count; i++) {
arr[left + i] = temp[i];
}
free(temp);
}
void mergeSortUpToDown(int* arr, int left, int right) {
if (left >= right) {
return;
}
int mid = (left + right) / 2;
mergeSortUpToDown(arr, left, mid);
mergeSortUpToDown(arr, mid+1, right);
merge(arr, left, mid, right);
}
由下往上的归并排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
void merge(int* arr, int left, int mid, int right) {
int* temp = (int*)malloc((right-left + 1) * sizeof(int));
int i = left;
int j = mid + 1;
int count = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[count++] = arr[i++];
} else {
temp[count++] = arr[j++];
}
}
while (i <= mid) {
temp[count++] = arr[i++];
}
while (j <= right) {
temp[count++] = arr[j++];
}
for (i = 0; i < count; i++) {
arr[left + i] = temp[i];
}
free(temp);
}
void mergeGroups(int* arr, int length, int gap) {
int i;
int lengths = 2 * gap; // 两个相邻的子数列的长度
// 将每 2 个相邻的子数列合并排序
for (i = 0; i + 2*gap < length; i += (2*gap)) {
merge(arr, i, i + gap - 1, i + 2*gap - 1);
}
// 若 i+gap-1 < length-1,则剩余一个子数列没有配对
// 将该子数列合并到已排序的数列中
if (i+gap-1 < length-1) {
merge(arr, i, i + gap - 1, length - 1);
}
}
void mergeSortDownToUp(int* arr, int length) {
int n;
if (length <= 0) {
return;
}
for (n = 1; n < length; n *= 2) {
mergeGroups(arr, length, n);
}
}